Круги на полях идентифицированы Crop circles are identified: Рисунки на полях-Проекции The drawings in the margins, projections

.2. Конструирование «золотого» равнобедренного треугольника, пентагона и додекаэдра

С какой целью Евклид ввел Предложение 2.12? Ответ на этот вопрос мы находим в статье [2]. Как показано в [2], Евклид использовал «Принцип Золотого Сечения», заложенный в «задаче о делении отрезка в крайнем и среднем отношении», для конструирования «золотого» равнобедренного треугольника, а затем «пентагона» и «додекаэдра».

Евклид конструирует «золотой» прямоугольный треугольник следующим образом (Рис.3). Возьмем отрезок AB и найдем на нем точку C, которая делит отрезок в «золотом сечении». После этого проведем дугу радиусом AB с центром в точке А. Найдем на дуге такую точку D, чтобы AC = CD = BD. Тогда треугольник ABD и будет искомым «золотым» равнобедренным треугольником, в котором углы при основании BD (72°) будут равны удвоенному значению угла при вершине А (36°).

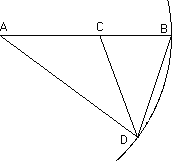
Рисунок 3. Геометрическое построение «золотого»
равнобедренного треугольника

Используя это геометрическое построение, Евклид затем строит «пентагон». Исходным для построения «пентагона» является «золотой» равнобедренный треугольникABD (Рис. 3). Проведем окружность через точки A, B и D (Рис.4). Проведя биссектрису угла ADB до пересечении с этой окружностью в точке Е, мы найдем четвертую вершинуЕ «пентагона». Заметим, что биссектриса DE проходит через точку С, которая делит отрезок AB в «золотом сечении». Аналогично, проведя биссектрису BF угла ABD до пересечения с окружностью в точке F, мы найдем пятую вершину F «пентагона», после чего можно нарисовать «пентагон» (Рис.4)

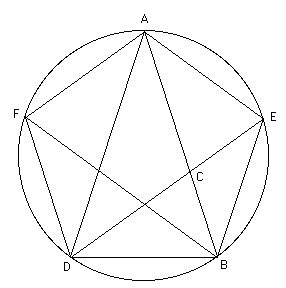
Рисунок 4. Геометрическое построение пентагона

Используя «пентагон» на Рис.4, Евклид затем строит «додекаэдр» (Рис.5). Важно подчеркнуть, что Евклид строит две «сакральные» фигуры, которые играли важную роль в учениях Пифагора и Платона. Как известно, «пентаграмма», которая лежит в основе «пентагона», являлась главным «сакральным» символом Пифагорейского союза, а «додекаэдр» в космологии Платона считался главным из пяти «Платоновых тел» и символизировал Гармонию Мироздания. Как подчеркивает Э.М. Сороко [3],«представление о «сквозной» гармонии бытия неизменно связывалось с ее воплощением в этих пяти симметричных геометрических телах, выражающих идею повсеместного совершенства мира вследствие совершенства каждой из составляющих его «стихий», «начал».

Рисунок 5. Додекаэдр

Видео на Русском языке
измерения
проекции
сферы
пространство
окружности
тор
преобразования

“3D рисунки мелом” настоящей флоры и фауны

художник Франсуа Абелане

Всмотритесь в этот рисунок,шестиугольник превращается в куб.

Перед вами изображен рисунок, на котором нарисованные со смещением круги синего и желтого цвета, что вы видите? Думаю, что не чего

, так как картинка статическая вы будите видеть обычные круги вложенные друг в друга, но как только придать фигуре движение, то я вам скажу, что ваше мнение поменяется. Ниже рисунка, я выложил анимацию вращающегося диска

Вращение диска создает трехмерную иллюзию. Может, с первого раза, вы не увидите, но через пару секунд иллюзия станет очевидной. Оптическая иллюзия будет более интенсивной, если вы будите смотреть только одним глазом.

http://illjuzija.ru/animaciya/kineticheskij-effekt-glubiny.html

Один из финалистов в соревнованиях оптического обмана 2010 года, Барт Андерсон из университета Сидней, Австралия, который занял второе место, своей гениальностью и простотой, продемонстрировал эффект парадоксальных иллюзорных контуров.

И, так перед вами четыре больших круга и четыре маленьких. На анимации Вы видите, что они двигаются противоположно друг от друга, и вот когда они пересекают границу квадрата наблюдается эффект полупрозрачных контуров. Тем самым образовывается, полупрозрачный квадрат, где углами его становятся маленькие круги.

На самом деле, прозрачных контуров не существует! Просто наш мозг как-бы прорисовывает недостающую информацию, чтобы обеспечить лучшее полное объяснения изображения, которые формируются в наших глазах.