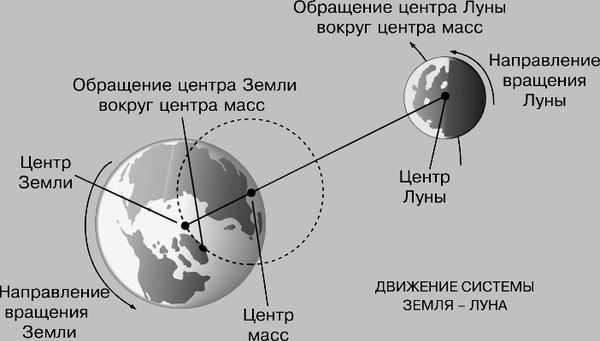
Центр тяжести Земли движется относительно центра масс системы Земля+Луна. Последний находится на линии, соединяющей центры масс Земли и Луны, на расстоянии, равном

|

|
2) Центр тяжести системы Земля+Луна движется вокруг Солнца по орбите, элементы которой не являются постоянными, а являются функциями времени. Орбита близка к круговой; эксцентриситет орбиты равен
3) Центр Солнца движется относительно центра тяжести солнечной системы - барицентра. Движение центра Солнца относительно барицентра солнечной системы определяется, главным образом, двумя наиболее массивными планетами - Юпитером и Сатурном и представляется двумя почти круговыми движениями с периодами обращения этих планет (
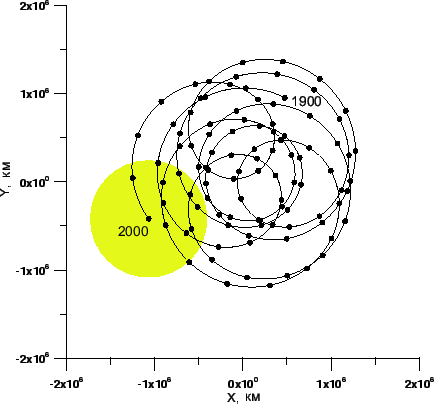 |
Рис. 3.16. Движение Солнца относительно барицентра солнечной системы в эклиптической системе координат на интервале времени 1900 - 2000 гг. Промежуток между точками равен одному году. |

Еще ближе к истине подошел выдающийся гелиофизик Теодор Ландшайдт, который открыл тесную связь между солнечной активностью и ускорением в движении барицентра солнечной системы [26-28] (см. рис. 2). Он определил, что именно максимум ускорения движения барицентра является спусковым механизмом солнечной активности и указал на неразработанность теории физики солнечного ядра.

Рис. 2. Движение барицентра солнечной системы за последние полстолетия, Landscheidt, 1976, [26].
Дейтерий, будучи стабильным элементом накапливается в солнечной атмосфере. Тритий также может накапливаться, если скорость его образования будет выше, чем скорость естественного распада и расхода на ядерные взрывы с реакциями синтеза гелия из изотопов водорода. Основной реакцией является
2D + 3T -> 4He + n + 17.6 MeV
Период полураспада трития 12.26 лет [29]. Отсюда можно сделать вывод, что при импульсном, то есть одновременном расходе трития, максимум следующей концентрации будет наблюдаться через 12±4 года в зависимости от скорости его образования. Так оно и есть. Циклы солнечной активности повторяются именно через такие промежутки или исчезают на десятилетия, пока не созреют условия для их возникновения, то есть если скорость накопления трития будет ниже скорости его распада. Один из таких минимумов, названный Дж. Эдди [30] Маундеровским минимумом, имевший место 1645 - 1715 годы, был открыт в 1852 году Й. Р. Вольфом [31, 32] и подробно описан Г. Шпёрером и Е. Маундером [33].
Как известно [34], это время климатологи называют “малой ледниковой эпохой” или “стадией Фернау” (название тирольского ледника), когда глобальная температура снизилась почти на 1o.
Исходя из изложенных выше соображений и фактов автор пришел к следующей схеме солнечной активности.
Раз в 8 - 16 лет у поверхности метатвердого солнечного ядра возникают условия инициации ядерных реакций синтеза гелия из протий-дейтерий-тритиевой газовой смеси. Эти условия возникают в момент наивысшей эмиссии нейтронов из метатвердого ядра. В этот момент вблизи ядра образуется много спонтанно делящихся изотопов тяжелых элементов, создающих условия цепной ядерной реакции и концентрация трития превышает критическое значение, необходимое для возникновения термоядерного взрыва.
Особенностью процесса является то, что основной DT-термоядерный процесс инициируется низкоэнергетическими ядерными реакциями более тяжелых элементов, насыщенных нейтронами, аналогично атомному запалу водородной бомбы. Это реально наблюдаемая фаза предвспышечного нарастания активности, “разогревающая” место будущего TD-взрыва. Согласно расчетам автора даже в центре Солнца в отсутствие взрывов температура не превышает 150000 oK [15].

Показано движение центра Солнца с 1940 по 2000 гг. Желтый круг – положение Солнца в 1990 г., когда его центр совпадал с центром масс системы – белая точка. С 1978 по 1986 гг. центр масс находился за пределами солнечного диска. В это время был “парад планет”. В последнее пятилетие XX века – центр тоже вне солнечного диска.
 |
| Перемещение центра Солнца относительно центра масс. |


Первым, достаточно очевидным результатом, является тот факт, что эллиптические траектории движения каждого из тел становятся невозможными.
Сила Кариолиса, действующая на каждое из тел системы, растягивает эллиптическую траекторию движения, и на каждом витке делает
ее более круглой, постепенно приближая эллиптическую траекторию движения к круговой.
2. В свою очередь, пара сил Кариолиса создают момент сил, заставляющих всю систему тел вращаться как единое целое вокруг центра масс системы.

Сила Кариолиса, действующая на каждое из тел системы, растягивает эллиптическую траекторию движения, и на каждом витке делает
ее более круглой, постепенно приближая эллиптическую траекторию движения к круговой.
2. В свою очередь, пара сил Кариолиса создают момент сил, заставляющих всю систему тел вращаться как единое целое вокруг центра масс системы.

Как показывают результаты численного моделирования движения "системы двух тел", разных типов траекторий движения, удовлетворяющих
всем законам Кеплера и всем законам сохранения, может быть быть достаточно много.
Например, на рисунке слева показана спиралевидная траектория "Спираль внутрь системы".
Желтая траектория движения показывает движение тела с большой массой (Земля на рисунке).
Красная спиралевидная кривая показывает движение тела с малой массой (Луна на рисунке).
Фон рисунка показывает аналогичную, но уже вполне реальную спиралевидную траекторию движения небесных тел (взята одна из
фотографий звездного неба из каталога NASA, журнала "Space" ).
В данном случае, начав свое движение на периферии, тела стремятся внутрь системы, постепенно
трансформируя траекторию своего движения в круговую траекторию.
Разумеется, время такой трансформации бесконечно велико, поскольку сила Кариолиса, при стремлении траекторий
движения к окружности, стремится к нулю.

Несколько иной тип траекторий показан на рисунке справа.
В этом случае начальные условия движения таковы, что тела первоначально удаляются друг от друга, но постепенно
их траектории движения тоже приобретают форму окружностей.
Как уже было сказано ранее, различных типов траекторий движения системы двух небесных тел, достаточно много.
Но самое интересное заключается в том, что среди всего многообразия РЕАЛЬНЫХ траекторий движения "системы двух тел" мы не обнаруживаем ни одной
"эллиптической" траектории движения.
Причем эллиптическую траекторию движения мы не обнаруживаем ни в "планетных системах", ни в системах "двойных звезд", ни в "системах спутников планет",
ни в любых иных системах.
Доминируют во всем этом "хаосе движений" круговые и спиралевидные траектории, а не эллиптические.
Разумеется, некоторое внешнее сходство с эллиптическими траекториями мы наблюдаем и в моделировании, и в реальной жизни.
Но "чистых" эллиптических траекторий движения, о которых нам говорили Кеплер, Гук и Ньютон, и в существовании которых
нас пытается убедить современная "классическая механика", мы не наблюдаем НИКОГДА.
